Key Difference: Sine and cosine waves are signal waveforms which are identical to each other. The main difference between the two is that cosine wave leads the sine wave by an amount of 90 degrees.

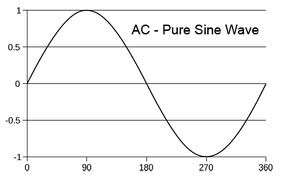A sine wave depicts a reoccurring change or motion. It is known as sine wave as it has the similar shape as the sine function, when it is plotted on a graph. The graph shows the repetition of one wave segment in a repeated manner.  The sine function is generally denoted by f(x)=a sin(bx+c)+d.

Where, a, b, c, and d are all constants, with a is not equal to zero

x is measured in radians

The function can be simply referred to as f(x)=sin(x), when a=b=1 and c=d=0

It can also be written in the form of f(t)= A sin(2 πωt + ϕ), where A=amplitude, ω = frequency and ϕ = phase or offset. 

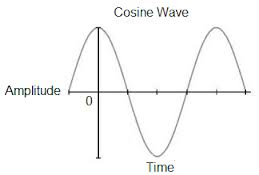Cosine wave is similar to a cosine function when depicted on a graph. One must know that sine and cosine waves are quiet similar. One can easily notice that every cosine function is basically a shifted sine function. The cosine function is moved to the left by an amount of π/2.

The equation of a cosine function is given by f(x)=a cos(bx+c)+d, where, a, b, c, and d are all constants with a is not equal to zero.

x is measured in radians  (π radians =180 degree, the angle measured of a half circle)

Therefore, cosine function and sine function are identical to each other, except with the horizontal shift to the left of π/2 radians in cosine function. Due to this similarity, any cosine function can be written in terms of a sine function as cos x=sin (x+ π/2). There is also no difference in the frequency of a cosine and its corresponding sine wave. Both have a maximum of 1 and a minimum of -1. Sine function curve stats at 0 and then moves upward to 1 by π/2 radians and then comes back to -1. On the other hand, the cosine curve starts at 1, comes down until π radians and then again moves upward.

Comparison between Sine and Cosine Wave:

Image Courtesy: reddit.com, learningaboutelectronics.com