Difference between Convex and Non-convex
Key Difference: Convex refers to a curvature that extends outwards, whereas non-convex refers to a curvature that extends inward. Non-convex is also referred to as concave.
 Convex and non-convex both define the types of curvature. Convex defines the curvature that extends outwards or bulges out. On the other hand, non-convex defines a curvature that extends or bends inward. Thus, the extension of the curve is used to differentiate between the two forms. Convex and non-convex are often used as adjectives to define the entities associated with the shape or curve defined by them.
Convex and non-convex both define the types of curvature. Convex defines the curvature that extends outwards or bulges out. On the other hand, non-convex defines a curvature that extends or bends inward. Thus, the extension of the curve is used to differentiate between the two forms. Convex and non-convex are often used as adjectives to define the entities associated with the shape or curve defined by them.
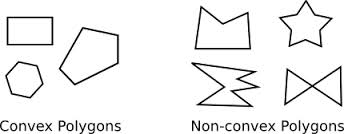
For example, in terms of a polygon, two general categories include convex and non-convex polygons. A convex polygon has no internal angle greater than 180 degrees. However, if a polygon exists with one or more internal angles greater than 180 degrees, then the polygon is known as the non-convex or concave polygon.
In Euclidean space, an object is convex if for every pair of points lying in the object, every point on the straight line segment that joins them also falls within the object. However, if any line segment falls outside the shape or set, then it is regarded to be non-convex. A solid cube is an example of convex, whereas a crescent shape is non-convex (concave).
The concept of convex and non-convex has also been extended to functions and variables to solve the related problems. Let f be a function of many variables defined on the convex set S. Then f is
(non convex) concave on the set S if for all x ∈ S, all x' ∈ S, and all λ ∈ (0,1) we have
f ((1−λ)x + λx') ≥ (1−λ) f (x) + λ f (x')
convex on the set S if for all x ∈ S, all x' ∈ S, and all λ ∈ (0,1) we have
f ((1−λ)x + λx') ≤ (1−λ) f (x) + λ f (x').
Convex and non-convex are also associated with lens and mirrors. A convex lens is the one which is thicker at the middle than the edges. On the other hand, a non-convex lens is thicker at the edges than the middle. Convex mirrors are the curved mirrors in which the silvered surface bulges outward. Non-convex mirrors contain an inward silver surface.
Therefore, the terms are used in context to many types of objects, but all are based on the basic definition of convex and non-convex.
Comparison between Convex and Non-convex:
|
|
Convex |
Non-convex |
|
Definition |
A convex curvature is rounded like the exterior of a sphere. |
A concave (non-convex) curvature is rounded inward |
|
Analogy |
Mountain |
Valley |
|
Polygon |
The two points lying in the polygon are connected by a line segment, and if that line segment also entirely lies in the polygon, then the polygon is considered a convex polygon. (Condition should hold true for all the points.) |
The two points lying in the polygon are connected by a line segment, and if that line segment does not entirely lies in the polygon, then the polygon is considered a non-convex polygon. (Condition should hold true for at least one pair of points.) |
|
Example |
Indifference curves are convex curves with respect to the origin. |
The inside of the spoon |
|
Other name |
Concave upward, convex downward |
Concave, concave downward, convex upward |
Image Courtesy: math.hws.edu









Comments
Anonymous
Tue, 12/05/2017 - 17:23
Anonymous
Wed, 05/17/2017 - 12:56
Add new comment