Difference between Convex and Concave Curves
Key Difference: A concave curve is rounded inward, whereas a convex curve is rounded like the exterior of a sphere.
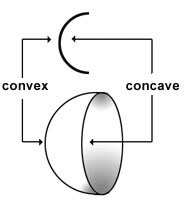 A curve is very different from a straight line. A curve has a varying slope. It is a wiggly line or bent line which wiggles or bends to join any two points on a graph or a map. Curves can be divided into categories of convex and concave curves. A concave curve rounds inward. On the other hand, a convex curve is rounded like the exterior of a sphere or a circle. Many people understand the terms by considering that a concave curve is similar to a valley and a convex curve is similar to a mountain. Thus, it helps in remembering the differences between the two.
A curve is very different from a straight line. A curve has a varying slope. It is a wiggly line or bent line which wiggles or bends to join any two points on a graph or a map. Curves can be divided into categories of convex and concave curves. A concave curve rounds inward. On the other hand, a convex curve is rounded like the exterior of a sphere or a circle. Many people understand the terms by considering that a concave curve is similar to a valley and a convex curve is similar to a mountain. Thus, it helps in remembering the differences between the two.
In a concave curve, a straight line connecting any two points on the curve lies entirely under the curve. However, in a convex curve, a straight line joining any two points lies totally above the curve. Both the curves are regarded opposite to each other. Therefore, a negative convexity refers to a term named as concavity. Concavity and inflection point describe the directions of a curve. Concavity describes the way that a curve bends. An inflection point is a point where the function has a tangent and the concavity changes. For example, if a curve is concave down (simply concave) then the graph of the curve is bent down, otherwise for the case of a concave up (convex) type of curve, the graph of the curve is bent upward. Convex and concave are often used to denote a gentle and subtle curve that is generally found in mirrors and lens.
Comparison between Convex and Concave Curves:
|
|
Convex Curves |
Concave Curves |
|
Definition |
A convex curve is rounded like the exterior of a sphere. |
A concave curve is rounded inward. |
|
Analogy |
Mountain |
Valley |
|
Directionality of a curve |
Concave upward - if the curve ‘bends’ upward |
Concave downward - if the curve ‘bends’ downward |
| Theorem |
If a function is concave up on a given open interval, then it is also continuous on it. (Let f be a real function which is differentiable on the open interval (a..b).) f is convex on (a..b) iff its second derivative D2f is ≥0 on (a..b) |
If a function is concave down on a given open interval, then it is also continuous on it. (Let f be a real function which is differentiable on the open interval (a..b).) f is concave on (a..b) iff its second derivative D2f is ≤0 on (a..b). |
|
Example |
Indifference curves are convex curves with respect to the origin. |
The inside of the spoon. |
Image Courtesy: fetchaphrase.com









Comments
Tom
Mon, 03/27/2017 - 21:29
Larry
Wed, 06/22/2016 - 18:18
Add new comment