Difference Between Expense and Asset
Key Difference: As can be seen from the definitions of both the terms, the key difference between an expense and an asset is timing. An asset represents any source of future economic benefit to the firm that goes beyond one year, whereas an expense is an item whose usefulness to the company is complete. The other main difference between an Expense and an Asset is that Expenses are deductible against income , so they reduce taxable income, but expenses cannot be depreciated ever and Assets are not deductible against income, but assets whose value decline over time (usually long-term assets) can be depreciated.
Expense:
Expense in accounting term is the money spent or cost incurred as part of a firm's operating activities during a specified accounting period. Expense represents the cost of doing business, where doing business is the sum total of the activities directed towards making a profit. Expenses can be in form of actual payments like salaries or wages or as a depreciated value of an asset or a certain amount used from earnings, which is also called as bad debts. Expenses are included in income statement as deductions from the income before assessing income tax. Expenses mostly included in Financial statements of the year the expenses have incurred excluding those capital expenditure and revenue expenditure. Expenses is the part of the cost that has expired and has been used up by activities directed at generating revenue. So, while all expenses are costs, but not all costs are expenses such as cost incurred in acquisition of income generating assets. For example, just as an inventory is an asset, so 'the cost of goods sold' becomes the expense, because this is the cost of inventory that was sold during the year.
Expenses are less costly and less expensive services or goods that a company procures in order to run business. Expenses directly reduce the taxable income in the year they are incurred or by paying using cash method in that year. Expenses are generally used in a shorter period of time. Following are the examples of Expenses, which include Rent, health insurance, food, clothes, entertainment, travel, office supplies, printer, utilities and cartridges.
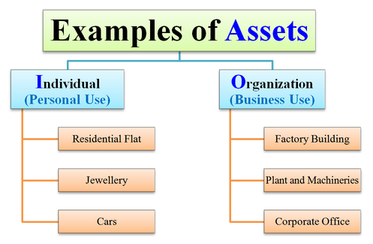Asset:
Assets are purchases that a business makes to help the company provide the products/goods or services that it sells. An asset is something which generates cash flow in near future by reducing expense and improving sales. An Asset is defined as, “An Asset is a resource with an economic value that an individual, corporation or country owns or controls with the expectation that it will provide a future benefit”. It represents economic resource of a firm or access of something which other entity or individual does not own. Assets are recorded in the balance sheet of the company and is based on the historical value or original cost of the asset with adjustments made for improvements. For example, inventory is an asset. Historical cost or value is also called as Book value'. In comparison to the expenses, assets are expensive and has useful life span of more than a year. The full cost of an asset is not written off in one year like it is done for an expense. Due to the fact that asset is expected to last multiple years, its cost is depreciated over multiple tax years. Purchases of such things like vehicle, buildings or equipment is not an expense and is considered as an asset, which are to be utilized over its useful life. These kind of purchases are also known as Capital expenditure items. Examples of assets are buildings, vehicle, machinery, plant, land, computer systems, etc.
Assets are also called as tangible resource as they belong to an individual or a business and has a value after a year or so and the best assets grow over time, but some also loose value over time. For example, the car looses or depreciates heavily in the first few years, whereas Real Estate generally goes up value.
Difference: The difference is of timing, as an asset brings benefit in sometimes near future and once when asset is used after the benefit, it becomes an asset. After the selling of inventory, the asset is then moved out of inventory account in balance sheet and is moved into Cost of Goods Sold (COGS)account in the balance sheet. Sometimes the asset does not provide benefit as it lost it's value before its use. So, then it is treated as an expense that is deducted in the income statement. If the inventory, somehow is damaged or is considered out of use, then it is recorded as a loss in the income statement.
Comparison Between Expense and Asset:
|
Particulars |
Expense |
Asset |
|
Definition |
Defined as an outflow of cash or money or assets to another individual or a firm as payment for an item or service |
An Asset is a resource with an economic value that an individual, corporation or country owns or controls with the expectation that it will provide a future benefit. |
|
Meanings |
Outflow of cash or cost or sacrifice incurred by the firm to earn the revenues |
Source of Income or something which the business owns |
|
Example |
Purchases, salaries to employees, purchase of stationery etc. |
Plant, Machinery, land and building, etc. |
|
Difference |
Expenses are cost of bringing in revenues. |
Provide future benefit and helping in bringing future profits and revenues. |
|
Duration |
Short period of time |
Usually longer duration with minimum of a year |
|
Cost |
Less expensive |
Costly investment |
|
Value |
Written (value) mostly immediately or at the time of purchase |
Usually written off over a period of time like a year. |
|
Types |
Fixed, Periodic or Variable expenses. |
Capital, Intangible and Current assets. |
Image Courtesy: Marketbusinessnews.com, Kalyan-city.blogpost.com
 |
 |
 |
 |
 |
 |
 |
 |
Add new comment