Difference between Trapezium and Parallelogram

Key Difference: A trapezium is a quadrilateral is that has at least one pair of parallel sides. The figure is more commonly known as a trapezoid. A parallelogram is a quadrilateral that has two pairs of parallel sides.

Trapezium/Trapezoid The words trapezium and parallelogram are commonly found in mathematics and geometry. These terms refer to geometric shapes that are commonly used to learn and understand angles. Both, trapezium and parallelogram are quadrilaterals and may result in it being confusing for people that are not actively using geometry. These figures also play an important part in architecture.

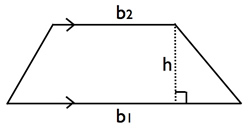
A trapezium is a quadrilateral is that has at least one pair of parallel sides. The figure is popularly known as trapezoid in most parts of the world, but referred to as trapezium in certain countries such as the UK. According to Math Open reference the name suggests other differences. A trapezium in the United States refers to a quadrilateral with no parallel sides, while a trapezoid refers to a quadrilateral that has one pair of parallel sides. However, in the UK it is considered the opposite; a trapezoid is considered to be a quadrilateral with no parallel sides, while a trapezium is considered to a quadrilateral with one pair of parallel sides.

The parallel sides of a trapezium/trapezoid are called the bases of the trapezoid and the other two sides are called the legs or the lateral sides. However, if the lateral sides of legs are parallel then the trapezoid would have two bases. There is some disagreement to the actual definition of trapezium, with some saying that a trapezium has exactly one pair of parallel sides, while others define a trapezium having at least one pair of parallel sides. According to the former definition, a parallelogram would not be considered as a trapezium, while the latter definition states that a parallelogram would be a special kind of trapezium.

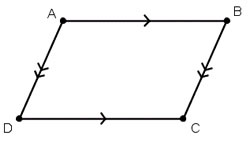
Parallelogram

A parallelogram is a quadrilateral that has two pairs of parallel sides. The opposite sides of a parallelogram are parallel to each other, hence the name has parallel in it. The opposite facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. A quadrilateral consists of square, rectangle and rhombus. A rectangle is a parallelogram with two pairs of parallel sides that makes four right angles of equal sides. A square is a parallelogram with four sides of equal length and four right angles of equal size. A rhombus is a parallelogram with four sides of equal length.

	Trapezium	Parallelogram
Type	Quadrilateral	Quadrilateral
Edges and vertices	4	4
Characterizations	A convex quadrilateral is a trapezoid if and only if it has two adjacent angles that are supplementary, that is, they add up 180 degrees. A convex quadrilateral is a trapezoid if and only if the angle between a side and a diagonal is equal to the angle between the opposite side and the same diagonal. A convex quadrilateral is a trapezoid if and only if the diagonals cut each other in mutually the same ratio (this ratio is the same as that between the lengths of the parallel sides). A convex quadrilateral is a trapezoid if and only if the diagonals cut the quadrilateral into four triangles of which one opposite pair are similar. A convex quadrilateral is a trapezoid if and only if the diagonals cut the quadrilateral into four triangles of which one opposite pair have equal areas. A convex quadrilateral is a trapezoid if and only if the product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal.	Two pairs of opposite sides are equal in length. Two pairs of opposite angles are equal in measure. The diagonals bisect each other. One pair of opposite sides are parallel and equal in length. Adjacent angles are supplementary. Each diagonal divides the quadrilateral into two congruent triangles. The sum of the squares of the sides equals the sum of the squares of the diagonals. (This is the parallelogram law.) It has rotational symmetry of order 2.
Properties	Four sides. At least one pair of opposite sides are parallel. Angles between pairs of parallel sides are supplementary. The parallel sides are the bases. The non-parallel sides are the legs. It has two pair of base angles. Properties of an isosceles trapezoid (a special type of trapezoid). The properties of trapezoid apply by definition (parallel bases). The legs are congruent by definition. The lower base angles are congruent. The upper base angles are congruent. Any lower base angle is supplementary to any upper base angle. The diagonals are congruent.	Diagonals of a parallelogram bisect each other, Opposite sides of a parallelogram are parallel (by definition) and so will never intersect. The area of a parallelogram is twice the area of a triangle created by one of its diagonals. The area of a parallelogram is also equal to the magnitude of the vector cross product of two adjacent sides. Any line through the midpoint of a parallelogram bisects the area. Any non-degenerate affine transformation takes a parallelogram to another parallelogram. A parallelogram has rotational symmetry of order 2 (through 180°). If it also has two lines of reflectional symmetry then it must be a rhombus or an oblong. The perimeter of a parallelogram is 2 (a + b) where a and b are the lengths of adjacent sides. The sum of the distances from any interior point of a parallelogram to the sides is independent of the location of the point.
Formulas (mathopenref.com)	Area: (Base 1 + Base 2)/ 2 x height Finding the height from the area: (2 x area)/ Base 1 + Base 2 Finding a base from the area: (2 x area/ height) – base	Perimeter: 2 (width + height)