Difference between Concave and Convex

Key Difference: Concave is used to describe any entity having an outline that curves inwards. On the other hand, convex is used to describe an entity having an outline or surface that bulges out. The terms are used as adjectives to describe the types of lens, mirrors, polygons, etc.

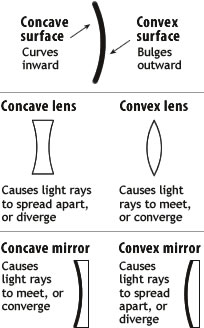
Concave and convex both are used as an adjective to denote an entity that has outline or surface curved inside or bulges outside. A concave surface is like the interior of a circle. On the other hand, a convex surface is similar to the exterior of a circle or sphere. Concave and convex are used in many lenses, mirrors, etc.

A concave lens is thinner in the middle and thicker at the edges. On the other hand, a convex lens is thicker in the middle and thinner at the edges. A convex lens is known as a converging lens, whereas a concave lens is also known as a diverging lens.

Concave and convex are also two types of spherical mirrors. A concave mirror is a spherical mirror in which the reflecting surface and the center of curvature fall on the same side of the mirror. On the other hand, a convex mirror is a spherical mirror in which the reflecting surface and the center of curvature lie on the opposite sides of the mirror.

The terms (concave and convex) are also used in context to polygons. A polygon with one or more interior angles greater than 180 degrees is referred to as a concave polygon. On the other hand, a polygon of which all interior angles are less than 180 degrees is known as a convex polygon.

Comparison between Convex and Concave Mirror:

	Concave	Convex
Mirror	A concave mirror is a spherical mirror in which the reflecting surface and the center of curvature fall on the same side of the mirror. In other words, if the mirror coating lies outside of the spherical surface, then it is known as a concave mirror.	A convex mirror is a spherical mirror in which the reflecting surface and the center of curvature lie on the opposite sides of the mirror. In other words, if the mirror coating lies in the inside of the spherical surface, then it is known as a convex mirror.
Lens	A convex lens focuses light rays.	A concave lens causes the light rays to diverge.
Meaning	Concave means “hollowed or rounded”.	Convex means “curved or rounded like the outside of a sphere or circle”.
Image for mirror (C stands for center of curvature, F for focal point and V for vertex)	Position of object (infinity) -> position of Image (At F) and Character of Image (Real, zero size) Position of object (between infinity and C) -> position of Image (Between F and C) and Character of Image (real, inverted, diminished) Position of object (AT C) -> position of Image (At C) and Character of Image (Real, inverted, same size) Position of object (Between C and F) -> position of Image (Between C and infinity). Character of Image (Real, inverted, magnified) Position of object (Between F and V) -> position of Image (From –infinity to V) and Character of Image (Virtual, upright, magnified) Position of object (AT V) -> position of Image (At V) and Character of Image (Virtual, upright, same size)	Position of object (infinity) -> position of Image (At F) and Character of Image (Virtual, zero size) Position of object (between infinity and V) -> position of Image (Between F and V) and Character of Image (Virtual, upright, diminished) Position of object (AT V) -> position of Image (At V) and Character of Image (Virtual, upright, same size)
Image for lens	Virtual, upright and smaller than the object between object and the lens (regardless of the object's position).	Real , inverted, smaller than object, - object at F Real , inverted, same size as object, - object at 2F Real , inverted, larger than object, object between 2F and F No image - object at F Virtual, upright, larger than object – behind object on the same side of the lens
Polygon	A polygon with one or more interior angles greater than 180 degrees is referred to as a concave polygon.	A polygon of which all interior angles are less than 180 degrees is known as a convex.