Difference between Matrix and Determinant
Key Difference: A matrix or matrices is a rectangular grid of numbers or symbols that is represented in a row and column format. A determinant is a component of a square matrix and it cannot be found in any other type of matrix.
Matrices and determinants are important concepts in linear mathematics. These concepts play a huge part in linear equations are also applicable to solving real-life problems in physics, mechanics, optics, etc. A matrix is a grid of numbers, symbols or expressions that is arranged in a row and column format. A determinant is a number that is associated with a square matrix. These two terms can become quite confusing for people that are just learning these concepts. Let’s try and understand them separately.
A matrix is a rectangular grid of numbers or symbols that is represented in a row and column format. Each individual term of a matrix is known as elements or entries. The matrix is determined with the number of rows and columns. For example, a matrix with 2 rows and 3 columns is referred to as a 2 x 3 matrix. Matrix can also have an even number of rows and columns; these are known as square matrix. Other forms of matrix include: row vector and column vector. A row vector is a matrix made up on only one row of numbers, while a column vector is a matrix that is made up of only one column of numbers.
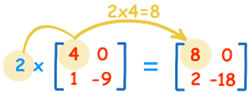
The matrices are usually enclosed in square or curved brackets. Each closed bracket is considered as a one matrix. These matrices are assigned a capital alphabet that represents the matrix. The data in the matrix can be any type of number that we choose, including positive, negative, zero, fractions, decimals, symbols, alphabets, etc. Matrices can be added, subtracted or multiplied. In case of addition, subtraction and multiplication of two matrices, the matrices must have the same number of rows and columns. There are two forms of multiplication: scalar multiplication and multiplication of a matrix by another matrix. Scalar matrix includes multiplying a matrix with a single number.
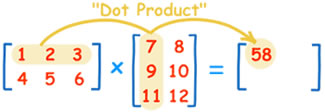
Multiplication of two matrices with each other requires solving them in a ‘dot product’, where a single row is multiplied with a single column. The resulting figures are then added up. The result of th first multiplication would be 1 x 7 + 2 x 9 + 3 x 11 = 58.
There are various different kinds of matrices: Square, diagonal and identity. A square matrix is a matrix that has the same number of rows and columns i.e.: 2x2, 3x3, 4x4, etc. A diagonal matrix is a square matrix that has zeros as elements in all places, except in the diagonal line, which runs from top left to bottom right. An identity matrix is a diagonal matrix that has all diagonal elements equal to 1.
Matrices are applied prominently in linear transformation, required for solving linear functions. Other fields that include matrices are classical mechanics, optics, electromagnetism, quantum mechanics, and quantum electrodynamics. It is also used in computer programming, graphics and other computing algorithms.
A determinant is a component of a square matrix and it cannot be found in any other type of matrix. A determinant is a real number that can be informally considered as the result of solving a square matrix. Determinant is denoted as det (matrix A) or |A|. It may seem like the absolute value of A, but in this case it refers to determinant of matrix A. The determinant of a square matrix is the product of the elements on the main diagonal minus the product of the elements off the main diagonal.
Let’s assume the example of matrix B:
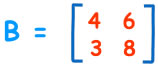
The determinant of matrix B or |B| would be 4 x 6 – 6 x3. This would give the determinant as 6.
For a 3x3 matrix, a similar pattern would be used.
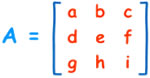
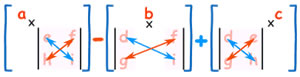
Richland Community College’s education website states there are various properties of determinants:
- The determinant is a real number, it is not a matrix.
- The determinant can be a negative number.
- It is not associated with absolute value at all except that they both use vertical lines.
- The determinant only exists for square matrices (2×2, 3×3, ... n×n). The determinant of a 1×1 matrix is that single value in the determinant.
- The inverse of a matrix will exist only if the determinant is not zero.
Images Courtesy: mathsisfun.com








Comments
mast
vishnu
Thu, 04/24/2014 - 14:24
Add new comment