Difference between Median and Average

Key Difference: Median is calculated by determining the middle or average of middle values in the sorted list of numbers. Average is calculated by adding all the numbers in the list and then dividing this number with the number of members in the list.

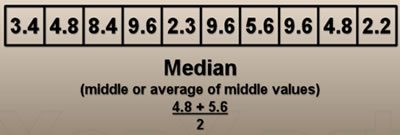Median and average, these terms are widely used in many fields. However, they are basic tools used in calculations in the field of mathematics and statistics specifically. Median defines the middle number of the group, when the group is arranged or ranked in order.

Median is simply the middle number in the list, but to use median, the numbers or group members must be defined or listed in rank or sorted order. In case, the provided list does not contain members in rank order, then the numbers should be first rewritten in rank order. When the number of members is odd, simply the middle member is selected as the median. On the other hand, if members are even in number, then the average of middle two numbers is considered to be the median.

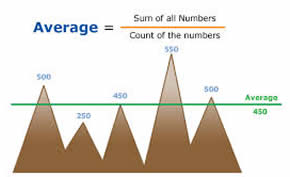On the other hand, average is derived by simply adding all the numbers of the group and then dividing this added value by the total number of members in the group. It is also known as arithmetic mean or average.

Let us consider an example –

This list of numbers contain 7 elements – (13,12,11,15,14,19,20)

To find out the average, first we just need to add all the numbers in the list –

13+12+11+15+14+19+20 =104

Now, simply divide this number by the total numbers in the group which is 7. Therefore, average = (104/7) = 14.85

To calculate median, one needs to first sort the numbers – (11,12,13,14,15,19,20)

The middle term in this case would be 14, as it falls right at the middle.

Average and median, are widely used in order to derive information about a population from the sample set of observed values. Average or mean should be used for situation when there are no extreme values in the data set. As otherwise, these values would effect mean and will not able to work as an effective measure of central tendency. On the other hand, median is preferred when there are extreme values in the data set, as it is not affected by the extreme values.

Comparison between Median and Average:

	Median	Average
Definition	Middle number or average of middle numbers in the sorted list of numbers	Also known as mean, obtained by dividing the sum of quantities by the number of quantities
Formula	n= total members in the list If n =odd Median = ((n+1)/2)th term If n=even Median = ((n/2)th term + (n/2+1)th term)/2	Sum of all data values/ number of data values
Extreme values in the data set	Preferred	Not preferred
Example in usage	Usually used in income level research	Usually used when the graph falls on a normal distribution