Key Difference: Radians and degrees are two different units for measuring an angle. The degree is the older way of measuring angles, dating back to the ancients. Radians are actually a more effective method of measuring an angle, albeit a bit more complicated. It is in fact the SI unit for measuring an angle, even if the degree is the more commonly used.

Radians and degrees are two different units for measuring an angle. The first thing any student of mathematics learns is how to measure an angle, whether it is a 45° angle, 90° angle, and so forth. Effectively, students are taught that angles are synonymous with degrees; however it is in advance study that we learn of radians.

Radians are actually a more effective method of measuring an angle, albeit a bit more complicated. It is in fact the SI unit for measuring an angle, even if the degree is the more commonly used.

The degree is the older way of measuring angles, dating back to the ancients. Each degree represents 1/360 of a full rotation. This means that each circle is divided into 360 degrees, and each movement is counted as 1°. So if we moved 5 times from the starting 0°, then it is five degrees, or 10°, then 15° and so forth until we reach back to 0 making a full 360° around the circle.

The actual reason of why the ancients divided the circle into 360 degrees is unsure, however the predominant theory states that the ancients believed the year was made up of 360 days, i.e. 12 months of 30 days each and each day the sun moved a little on the horizon from where it was the previous day, i.e. 1°. Also, the 360 degrees makes it somewhat simpler to break down the circle. Hence, half a circle its 180°, a quarter circle is 90°, then 45°, and so forth.

However, this system is somewhat limited. Firstly, the 360° system does not translate well into most other mathematical calculation, as they are not based on the 360 system. Hence, the radian came into play. The radian was in use since as long ago as the 1400s; however it was not adopted as an accepted unit until the late 1800s.

The concept of a radian is a bit more complicated then the degree. The radian is based on the radius of a circle. The radius of a circle is any line drawn in the circle that connects the center of the circle to the circumference. This line is then taken and measured around the circumference of the circle, when the beginning point of the line and the end point of the line are connected to the center, the lines form an angle. This angle is known as one radian. This radian can then be measured into the circle to see how many radians it takes to measure one circle. The answer is not straightforward.

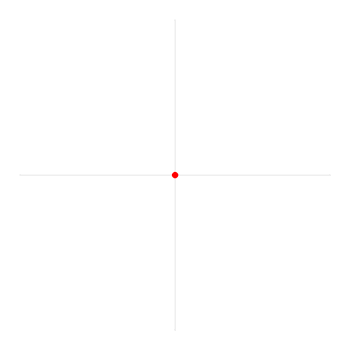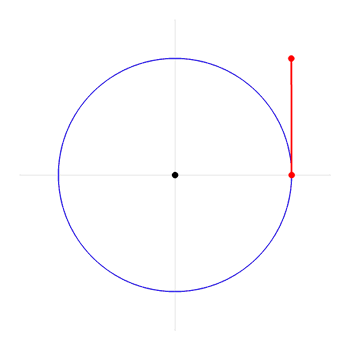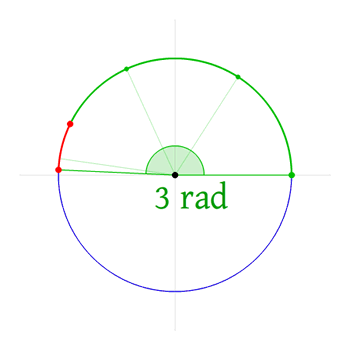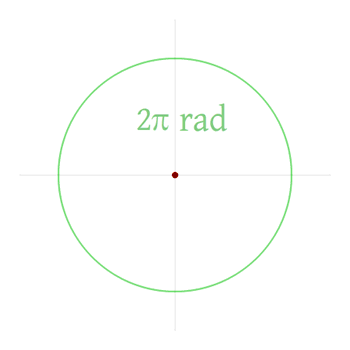
It takes 3 radians to form almost half of a circle. However, even after 3 radians, there is a little bit of the circumference left over. Hence, the official measurement is that a half of the circle equals to 3.14 radians or 3.14 rad. This is commonly written as π rad or πr. Hence, one circle equals to 2πr.

Since, one circle equals to 2πr, and we know that one circle equals 360°. Hence, it can be written that 2πr equals to 360°.

2πr = 360°

πr = 180°

1r = 180°/π

r = 180°/3.14 (as π = 3.14)

Hence, 1r ≈ 57.295

This can be used to convert between radians and degrees. However, this table can help with some of the more common conversions.

Comparison between Radian and Degree:

Image Courtesy: mathsisfun.com, wikipedia.org