Difference between Mean and Median
Key difference: Mean and median are two values that are commonly used in mathematics and statistics. The mean is essentially just another name for the average. The median, on the other hand, is the numerical value which falls in the middle of a sorted number set.
 Mean and median are two values that are commonly used in mathematics and statistics. The mean is essentially just another name for the average. There are exceptions to this; however, in basic mathematics mean is the same for average. The mean is calculated by adding all of the values together, then dividing by the number of original values.
Mean and median are two values that are commonly used in mathematics and statistics. The mean is essentially just another name for the average. There are exceptions to this; however, in basic mathematics mean is the same for average. The mean is calculated by adding all of the values together, then dividing by the number of original values.
The median, on the other hand, is the numerical value which falls in the middle of a sorted number set. Wikipedia defines median as “the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one. If there is an even number of observations, then there is no single middle value; the median is then usually defined to be the mean of the two middle values.”
The difference between mean and median would be better understood by studying examples.
Example of mean:
Number set: {12, 4 and 5}
So we add the numbers: 12+4+5 = 20
Then we divide by the number of values in the set, which in this case is 3: 21/3 = 7
Hence, the mean of {12, 4 and 5} is 7
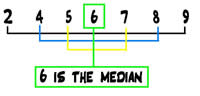
Example of median in odd set of numbers:
Let’s take the same number set.
Number set: {12, 4 and 5}
First we arrange the number set in increasing order: 4, 5, 12
The middle number of the set is 5, so the median is 5.
 Example of median in even set of numbers:
Example of median in even set of numbers:
Number set: {12, 4, 8 and 5}
First we arrange the number set in increasing order: 4, 5, 8, 12
As there is no single number falling in the middle of the set, the median will be the mean or average of the two middle numbers, which in this case is 5 and 8.
Calculate mean of 5 and 8: 5+8 = 13/2 = 6.5.
So, the median of {12, 4, 8 and 5}is 6.5.
One might wonder that the mean gives us the average of the set, so what is the purpose of calculating the median and why would it be used. The Australian Bureau of Statistics gives a simple example of the need for calculating median:
Example: Comparing the mean and the median
If students attending a tutorial group were aged 18, 18, 19, 19, 21, 22 and 51,
the mean age of the group would be 18 + 18 + 19 + 19 + 21 + 22 + 51 = 168 / 7 = 24
the median age of the group would be the middle value of 19.
Which age best represents the average age of the group? In this case, the mean age is distorted by the presence of the mature age student. The median age would be a closer indication of the true average age of the tutorial group.
Image Courtesy: mathsteacher.com.au, room17math.wikispaces.com








Add new comment