Key Difference: Geometrical shapes cover all basic shapes like lines, polygons and simple curves. Commonly, shapes are divided into three categories – 1, 2 and 3 dimensional shapes.

Shape defines the external boundary or surface of an object. Shapes in context to geometrical shapes lie in the concepts of plane and solid geometry. These geometric shapes provide the geometric location which excludes the factors like orientation, scale, location and reflection.

 These geometrical shapes can be classified into following categories –

1 Dimensional shape (Only Length)–

Line – The category  of 1 dimensional shapes includes shapes with only lengths. Line is the only 1 D shape. It can be a straight or a wavy line. Here the one dimension term refers to length.

2 Dimensional shapes (shapes with length and breadth) – A plane 2 D shape with straight lines and no curves is known as a polygon. A polygon with all sides and angles same is known as a regular polygon, and if not then it is termed as an irregular polygon. Some common examples are -

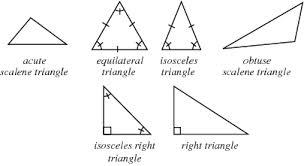
Triangles – These are shapes characterized by three sides. There are many different types of triangles like equilateral triangle with all sides equal in length and 3 equal angles of 60 degrees. Isosceles is another type of triangle which has 2 equal sides and 2 equal angles. Scalene triangle is the triangle which has no equal sides and no equal angles. It also includes a right angle triangle whose one of the angles is a right angle or of 90 degrees. Obtuse triangle is the triangle whose one of the angles is greater than 90 degrees, whereas the other two angles measure less than 90 degree. Acute triangle is the triangle whose all angles are acute.

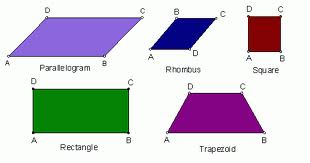Quadrilaterals – It is a close figure possessing 4 sides. This is a group consisting of a variety of members. Square is a quadrilateral with 4 equal sides and four right angles. They also possess 4 lines of symmetry. Rectangle is another quadrilateral with 2 lines of symmetry. It also possesses four right angles. A rhombus type of quadrilateral is characterized by 4 equal sides. Both pairs of opposite sides are also parallel in the case of rhombus. A parallelogram is the quadrilateral with 2 pairs of parallel sides. Rectangles, rhombus and square, all fall in the category of parallelogram. Trapezium possesses one pair of parallel sides of unequal lengths. 

Pentagon is a polygon with 5 sides, hexagon is a polygon with 6 sides, heptagon is a polygon with 7 sides, Octagon is a polygon with 8 sides. Similarly, nanogon contains 9 sides and decagon contains 10 sides.

Shapes with Curves – Some common examples are -

Circle – A circle is represented by three attributes – circumference, diameter and radius. It is basically a locus of all points which measure the same from a central point. Circumference denotes the total distance around the circle. Diameter is the longest distance calculated from one end of the circle to the other and radius measures the distance from center of circle to any point present on its circumference.

Ellipse – An ellipse is the cross section shape which is derived when a cone or a cylinder is cut at an angle. An ellipse is characterized by two points known by the same name as focus. The sum of distances to the focus points from any point on the ellipse remains same. It appears like a squashed circle reduced to an oval type shape. In this way, circle can be considered as a type of ellipse with major and minor axis of same length and both foci falling in the center.

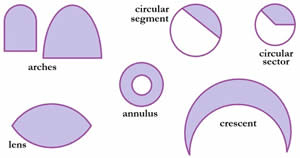Oval – It is used to denote any kind of closed egg shape or oblong curve with no points. This generic term can be used for ellipses as well as. It covers regular or irregular egg shaped curves too.

Arch – it is defined as a curved path from one point of a circle to another. It can be considered as a part of the circumference of a circle. An arc is known as major arc if it measures greater than 180 degrees, and if not then it is known as a minor arch.

Lens – It is a biconvex shape which is composed of two circular arcs meeting with each other through their end points. A symmetric lens is the one in which arcs have equal radii, whereas asymmetric les contain arcs with unequal radii. It can also be known as convex-convex type of shape.

Annulus – It is the shape of a ring which is formed when the smaller disk from the center is removed from the center of a disk. The word annulus has been derived from the Latin word which means little ring.

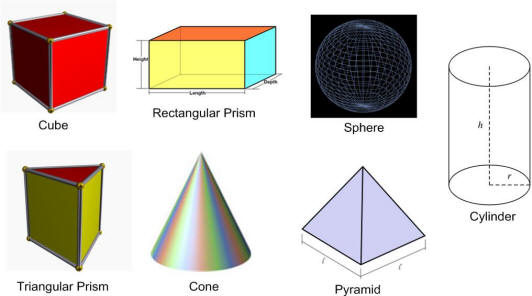3 D geometric shapes – These are solid shapes consisting of three dimensions which are length, breadth and height. Some common examples are –

Prism – Prism refers to the solid object possessing two congruent and parallel faces. A rectangular prism is the prism with rectangular bases. It has six faces and all faces meet at 90 degrees. The opposite sides of rectangular prism are parallel. Cube is also a prism but with six congruent faces. It is also known as a member of rectangular prisms. A Triangular Prism possesses triangular bases. Bases are only parallel in this type of prism. Hexagonal Prism is a prism whose bases are hexagonal and opposite faces are parallel.

Pyramid – It is a polyhedron whose base is a polygon with all lateral faces as triangles in shapes. One of the common pyramid shape is the one in which lateral faces are congruent. They are also known as right pyramids. The name of pyramid is mostly described by the shape of its base. For example – a hexagonal pyramid has a base of a hexagon.

Cylinder - The shape of the cylinder is described by flat base and flat top with one curved side. Base, top and in between region is same. If the middle section of a cylinder is unwrapped and put it flat then it will come out as a rectangle. It can be considered similar to a prism. However unlike prisms, its bases are circles but not polygons.

Cone – it is a curved shape which is characterized by a circular or oval base which gets narrower towards a point. A cone has only one vertex. A cone can also be considered as a pyramid with a circular cross section. A cone whose vertex is positioned above the center of its base is also known as the right cone.

Sphere – It is symmetrical in true senses with no edges or vertices. The distance from any point on the source to the center remains the same. Earth’s shape is almost spherical. However, it is known as spheroid shaped as it is not in the perfect shape of a sphere.

Image Courtesy: schoolatoz.nsw.edu.au, tdittrich.blogspot.com, xpmath.com, calculus-geometry.hubpages.com, mathwithlarry.com