Difference between Circle and Ellipse

Key difference: A Circle and Ellipse have closed curved shapes. In a circle, all the points are equally far from the center, which is not the case with an ellipse; in an ellipse, all the points are at different distances from the center.

Mathematically, a circle is a major shape in the field of geometry and its definition states: a circle is a shape with all points at the same distance from its center. It is named by its center. Some real world examples of a circle are wheels, a dinner plate and (the surface of) a coin.

The word ‘circus’ is derived from the Greek term ‘kirkos’, which is a metathesis of the Homeric Greek and means ‘hoop’ or ‘ring’. The circle has been known before recorded history. The Sun and the Moon are natural examples of a circle, whereas even a short stalk blowing in the wind, forms the shape of a circle in the sand. The principle of a circle was applied in the formation of wheels and gears by the pre-historic man. Now in the modern era, there are enumerable varieties of machineries based on the circle shape. The study of a circle and its development is applicable in the fields of mathematics, geometry, astronomy and calculus.

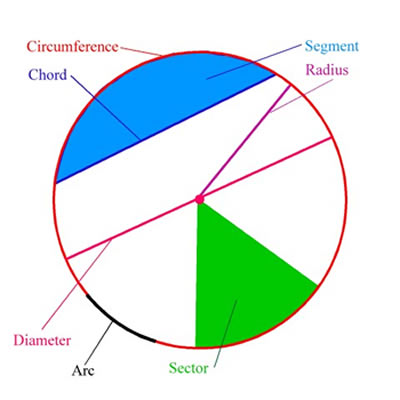
Circle

The following terms are involved in circle terminology:

Arc: any connected part of the circle.

Centre: the point equidistant from the points on the circle.

Radius: a line segment joining the centre of the circle to any point on the circle itself; or the length of such a segment, which is half a diameter.

Diameter: a line segment whose endpoints lie on the circle and which passes through the centre; or the length of such a line segment, which is the largest distance between any two points on the circle. It is a special case of a chord, namely the longest chord, and it is twice the radius.

Circumference: the length of one circuit along the circle.

Chord: a line segment whose endpoints lie on the circle.

Tangent: a coplanar straight line that touches the circle at a single point.

Semicircle: a region bounded by a diameter and an arc lying between the diameter's endpoints. It is a special case of a circular segment, namely the largest one.

Circular sector: a region bounded by two radii and an arc lying between the radii.

Mathematically, an ellipse is a common shape in the field of mathematics. Its definition states: a curved line forming a closed loop, where the sum of the distances from two points (foci) to every point on the line is constant. The real life examples of an ellipse are: a hula hoop, a glass of water, and a simple dinner plate when tilted to view at an angle.

Apollonius of Perga gave the name ‘ellipse’ in his Conics, which emphasizes the connection of a curve with the application of areas. It is a curve on a plane surrounding two focal points such that a straight line drawn from one of the focal points to any point on the curve and then back to the other focal point has the same length for every point on the curve. Its shape is represented by its eccentricity, which is arbitrarily close to 1. The study of ellipse and its properties are commonly applicable in the field of physics, astronomy and engineering. The orbits of planets with the Sun at one of the focal points, the moons orbiting the planets, and other systems having two astronomical bodies are the general examples of elliptical paths. The shape of planets and stars are often well described by ellipsoids. The ellipse is also considered as the simplest Lissajous figure, formed when the horizontal and vertical motions are sinusoids with the same frequency.

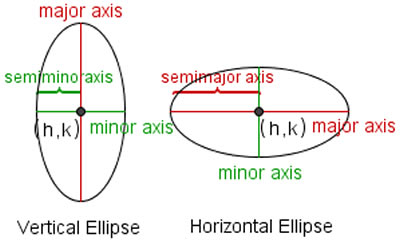
Ellipses

The terms involved mainly in the terminology of ellipse are:

Focus: The distance from the center, and is expressed in terms of the major and minor radii.

Eccentricity: The eccentricity of the ellipse (commonly denoted as either e or ε) is expressed in terms using the flattening factor.

Directrix: it is a line parallel to the minor axis, and with which each focus is associated.

Latus rectum: The chords of an ellipse which are perpendicular to the major axis and pass through one of its foci are called the latus rectum of the ellipse.

Major / Minor axis: The longest and shortest diameters of an ellipse. The length of the major axis is equal to the sum of the two generator lines.

Semi-major / Semi-minor axis: The distance from the center to the furthest and closest point on the ellipse. Half the major/minor axis.

Chords: The midpoints of a set of parallel chords of an ellipse are collinear.

Circumference: it is associated with the length of the semi-major axis and the eccentricity and is an integral part of an ellipse.

Comparison between Circle and Ellipse:

	Circle	Ellipse
Definitions	A circle is a round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the centre).	An ellipse is a regular oval shape, traced by a point moving in a plane so that the sum of its distances from two other points (the foci) is constant, or it is resulted when a cone is cut by an oblique plane, which does not intersect the base.
Variations	Circles do not vary in shape; they remain the same shape, even when the view is changed.	Ellipses vary in shape from very broad and flat to almost circular, depending on how far away the foci are from each other.
Radius consistency	It has a constant radius throughout the shape.	It does not have a constant radius throughout the shape.
Main components	Circle has one radius, which lies at the center.	Ellipse has two foci, which are at the either ends.
Area	π × r^2 Where ‘r’ is the radius of the circle.	π × a × b Where ‘a’ is length of the Semi-major Axis, and ‘b’ is the length of the Semi-minor Axis.
Standard equations	(x-a)^² + (y-b)^² = r^²	x^²/a^² + y^²/b^² = 1
Resemblance	Circles are the unique shapes, from which the other shapes originate.	Ellipses also arise as images of a circle under parallel projection and the bounded cases of perspective projection.