Difference between Concave and Convex Polygons

Key Difference: A polygon whose all interior angles are less than 180 degrees is known as a convex polygon. On the other hand, a polygon with one or more interior angles greater than 180 degrees is referred to as a concave polygon.

A polygon can be defined as a closed plane figure (a two dimensional shape) that consists of three or more line segments. Polygons can be divided into many types. One such type is based on the internal angles. A convex polygon is the one in which none of the angles point inwards. In other words, it has no internal angle that is greater than 180 degrees.

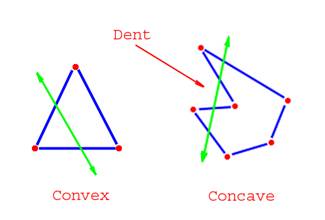A polygon with any of the internal angles greater than 180 degrees is known as a concave polygon. In other words, a concave polygon exists with an interior reflex angle. A simple line test can be used to distinguish a concave polygon with a convex polygon. If a line is drawn that passes through the polygon, and it always passes through only two of the lines or polygons making up the shape, then in that case, the shape of the polygon is convex. On the other hand, if the same process is repeated in a concave shape, then the line is able to pass through more than two of the lines. In 3 dimensional shapes, the same test can be performed to differentiate between the two.

It is important to note that all the diagonals of a convex polygon lie entirely inside the polygon. However, in a concave polygon, some diagonals will always lie outside the polygon. All regular polygons are convex (a polygon that has all sides equal and all interior angles equal). Convex polygons are easier to draw in comparison to concave polygons.

Comparison between Convex and Concave Polygons:

	Concave Polygon	Convex Polygon
Definition	A polygon with one or more interior angles greater than 180 degrees is referred to as a concave polygon.	A polygon of which all interior angles are less than 180 degrees is known as a convex polygon.
Properties	At least one interior angle is greater than 180 degrees It can be cut into a set of convex planes. A polygon that is not a convex polygon is referred to as a concave polygon.	Every internal angle is less than 180 degrees. Every line segment between two vertices of the polygon does not go exterior to the polygon (i.e., it remains inside or on the boundary of the polygon). Any vertical or horizontal axis intersects it at most twice.
Recognizing feature	A dent (curve inward)	All of its lines curve outside
Distinguishing Feature	A line does contain a side of the polygon containing a point on the interior of the polygon.	No line that contains a side of the polygon contains a point in the interior of the polygon.
Ways to create	Many	Comparatively few
Cross product	Cross product of adjacent vector pairs is <0	Cross-product of adjacent edges will be of same sign (that is, the z-component)
Example	The outline of the letter "W"	Triangle