Key Difference: A parabola is a conic section that is created when a plane cuts a conical surface parallel to the side of the cone. A hyperbola is created when a plane cuts a conical surface parallel to the axis.

Parabola and hyperbola are two different words, sections and equations that are used in mathematics to describe two different sections of a cone. These are different in shape, size and various other factors in including formulas that are used to calculate it. In order to understand them, let’s first understand the cone and the different conic sections.

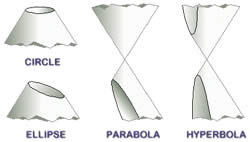A conic section is a curve that is obtained when a plane intersects with a cone in various different ways. The cuts that are obtained from the intersection include ellipse, circle, parabola and hyperbola. According to analytic geometry, conic is defined as, “a plane algebraic curve of degree 2.” The popular definition of conic section includes a focus point, directrix line and eccentricity.  The focus point and the directrix lines are expected to be in a fixed ration in a conic. The ratio is known as the eccentricity of the conic section. The eccentricity of ellipses, parabolas and hyperbolas differ; ellipses have an eccentricity less than 1, parabolas has an eccentricity that is equal to 1 and hyperbolas have an eccentricity of greater than 1. The earliest known work on conic sections can be dated back to the fourth century BC by Menaechmus, who discovered a way to solve the problem of doubling the cube through the use of parabolae.

A parabola is a conic section that is created when a plane intersects with a cone. Parabolae or parabolas form ‘from the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface.’ Another way a parabola is created is when a locus of points on a plane that are equidistant from the focus and the directrix create a parabola. In algebra, parabolas are commonly used in graphs of quadratic functions, using the formula y=x^2.

A line that splits the parabola through the middle is known as the axis of symmetry; this line is also perpendicular to the directrix and passes through the focus. The points that are on the axis of symmetry that intersect the parabola are called ‘vertex’. The distance between the vertex and the focus is known as the ‘focal length’. Parabolas can open in either direction including up, down, right or left. Also a main feature of parabolas is that they are all the same, only differing in size. They can be repositioned and rescaled exactly to fit any other parabola. Parabolas are used in various applications such as automobile headlight reflectors, design of ballistic missiles, etc. They also play a major role in physics, engineering, mathematics, etc.

Hyperbolas are a smooth curve that occurs when a plane intersects with the cone parallel to the y axis that creates a cut along the side of the cone. A hyperbola is defined by its geometric properties or equations for which it is a solution set. The term ‘hyperbola’ is derived from the Greek word which means “over-thrown” or “excessive”. The term is believed to be coined by Apollonius of Perga, who has contributed greatly to the study of conic sections.

A hyperbola is known to have branches that are mirror images to each other and resemble two infinite bows. The points on the two branches that are closest to each other are called the vertices. The line that connects the vertices is known as the transverse axis or major axis, which corresponds to the major diameter of an ellipse. The midpoint of a transverse axis is known as the hyperbola’s center.  The equation of a hyperbola is written as x2/a2- y2/b2= 1. Hyperbolas are used in various applications in today’s world including the path followed by the shadow of the tip of a sundial, the shape of an open orbit; it is used as an arch in many constructed buildings, as equations in mathematics and geometry, physics, etc.

Hyperbolas and parabolas are both open curves, meaning that they do not end and continue indefinitely to infinity, something that ellipses and circles cannot do. 

Image Courtesy: jwilson.coe.uga.edu, allmathwords.org