Difference between Sequence and Series

Key Difference: A sequence is an ordered list of numbers or terms. It can contain elements, numbers and terms and can be a limited set or an infinite set. A series on the other hand is the sum of a sequence.

Series and sequences are most commonly heard of in mathematics and statistics. They also make up a huge part in physics, computer science, and finance. Though in the English language as words these are interchangeable, in mathematics the definition of a sequence and a series differ greatly. A sequence is simply an ordered list of numbers or terms. A series is the sum of a sequence.

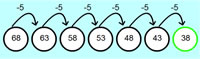
A sequence is an ordered list of numbers or terms. It can contain elements, numbers and terms and can be a limited set or an infinite set. Unlike in a set, order in a sequence has grave importance. It is known as a discrete function. For example [1, 2, 3, 4…] is a sequence or progression (in the UK). There are two types of sequence an arithmetic sequence and a geometric sequence. An arithmetic sequence is a sequence in which the difference between two consecutive terms remains constant, known as common difference. In a geometric sequence, the ratio between two consecutive terms remains constant, known as common ratio.

Sequences can be finite or infinite, such as the sequence of all even positive integers (2, 4, 6...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context. The sequence can also be in accessing order or descending order. It usually follows a pattern which can easily be figured out. A sequence may be named or referred to as "A" or "An". The terms of a sequence are commonly named as something like "ai" or "an", with the subscripted letter "i" or "n" being the "index" or counter. Example: A2 is the second place in the sequence will A6 denotes the six place in the sequence.

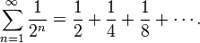A series on the other hand is the summation of a sequence. It is indicated with a either the Latin capital letter "S" or the Greek letter that corresponds to S, known as Sigma ‘∑”. It is usually the sum of a set sequence.

For example the summation of the first through tenth terms of a sequence would be written as 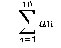. This would denote that the lower index of the sequence is 1; while the upper index on the sequence is 10, meaning the last term in the series will be a10.