Difference between Differentiation and Integration
Key Difference: In calculus, differentiation is the process by which rate of change of a curve is determined. Integration is just the opposite of differentiation. It sums up all small area lying under a curve and finds out the total area.
 Differentiation and Integration are two building blocks of calculus. Differential calculus and Integral calculus are just the opposite of each other. Differential calculus is basically dealing with the process of dividing something to get track of the changes. On the other hand, Integral calculus adds all the pieces together.
Differentiation and Integration are two building blocks of calculus. Differential calculus and Integral calculus are just the opposite of each other. Differential calculus is basically dealing with the process of dividing something to get track of the changes. On the other hand, Integral calculus adds all the pieces together.
Differentiation deals with the calculation of a derivative which is the instantaneous rate of change of function taking into one of its variables into consideration. It deals with quantities which continuously vary. In other words, it is equivalent to the slope of the tangent line, which is represented by m = change in y/ change in x.
It can be understood by this example – if there exists a function f(x) possessing an independent variable x, then in case x is increased with a small amount which would be delta x. Then, the same change will be reflected in the function too as delta f. The ratio delta f/delta x calculates this rate of change of function with respect to variable x.
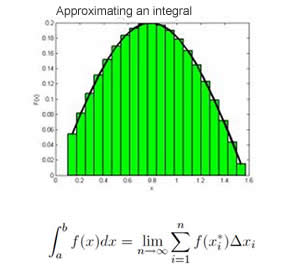 Integration is just the opposite of differentiation, and therefore is also termed as anti-differentiation. It is able to determine the function provided its derivative. It measures the area under the function between limits. The process of integration is the infinite summation of the product of a function x which is f(x) and a very small delta x. In context to a curve, it provides the total area under the curve from the x axis to the curve from a specific range. It is depicted by the symbol ∫. If the specific interval is mentioned then it is known as definite integral otherwise indefinite integral.
Integration is just the opposite of differentiation, and therefore is also termed as anti-differentiation. It is able to determine the function provided its derivative. It measures the area under the function between limits. The process of integration is the infinite summation of the product of a function x which is f(x) and a very small delta x. In context to a curve, it provides the total area under the curve from the x axis to the curve from a specific range. It is depicted by the symbol ∫. If the specific interval is mentioned then it is known as definite integral otherwise indefinite integral.
As integration and differentiation are just the inverse of each other, the integration may provide the original function if derivative is known. It is also described as the fundamental theorem of calculus. Differentials is all about differences and divisions, whereas integration is all about addition and averaging. Differential determines the function of the slope as the distance between two points gets very small, similarly the process of integration determines the area under the curve as the number of partitions of rectangles lying under the curve gets large.
Comparison between Differentiation and Integration:
|
|
Differentiation |
Integration |
|
Difference |
It is used to find the change in function with respect to the change in input |
The reverse process or method of differentiation |
|
Based on |
Dividing |
Integrating |
|
Determines |
Speed of the function |
Distance travelled by the function |
|
Graph |
Slope of the function |
Area between the function and the x axis |
|
Example |
For y=x to the power of 4 dy/dx=4 (x raise to the power of 3) |
Integration of 4 (x raise to the power of 3) is equal to = x to the power of 4 |
|
Formula |
The derivative of a function f(x) with respect to the variable x is defined as
|
The Definition for the Integral of f(x) from [a,b]
|
|
Application |
To determine a function is increasing or decreasing, calculation of instantaneous velocity |
Used to find areas, volumes, central points, etc |
Image Courtesy: maths.nayland.school.nz, littleengineers-fla.com

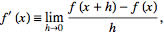
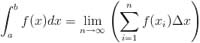







Comments
John
Thu, 10/05/2017 - 02:42
Add new comment